63 Reduction formula (EMBHJ) Any trigonometric function whose argument is \(\text{90}\text{°}±\theta\);Evaluate limit as theta approaches 0 of (cos(2theta)tan(2theta))/theta Tap for more steps Rewrite in terms of sines and cosines Combine and Take the limit of each term Tap for more steps Multiply the numerator by the reciprocal of the denominator Multiply and Move the limit inside the trig function because cosine is continuousFree math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor

Tan1 2 Sin 1 2x 1 X 2 Cos 1 1 Y 2 1 Y 2 X Y 1 Xy If X Lt 1 Y Gt 0 And Xy Gt 1 Mathematics Topperlearning Com Exkwfcdd
What is cos 2 theta formula
What is cos 2 theta formula-Tan theta * cos theta, simplify to a single expressionDouble angle formulas for sine and cosine sin 2t = 2 sin t cos t cos 2t = cos 2 t – sin 2 t = 2 cos 2 t – 1 = 1 – 2 sin 2 t Less important identities You should know that there are these identities, but they are not as important as those mentioned above They can all be derived from those above, but sometimes it takes a bit of work to do


Important Trigonometric Identiti
The first shows how we can express sin θ in terms of cos θ;Jun 05, · The given formula is $$ 0 = \cos{2\theta} \sin{2\theta}\tan{\phi} $$ And it is simplified to $$ \theta = \frac{1}{2}\tan^{1}{\left(\frac{1}{\tan{\phi}}\right)} $$ I don't really see how you can get there from the given foruma I've tried moving things around in the equation but it never gives me the proper resultMay 30, 18 · In this section we look at integrals that involve trig functions In particular we concentrate integrating products of sines and cosines as well as products of secants and tangents We will also briefly look at how to modify the work for products of these trig functions for some quotients of trig functions
Edit Beaten to itAnswer to If x= 5\tan \theta, express the following expressions in terms of "x" 1 \sin \theta\\ 2 \cos 2\theta\\ 3 \theta By signing up,Trigonometry Trigonometric Identities and Equations Fundamental Identities 1 Answer
The square of tan of angle is written as tan 2 θ and the cosine of double angle is written as the cos 2 θ in trigonometric mathematics The cosine of double angle is equal to the quotient of the subtraction of square of tangent from one by the sum of one and square of tan functionMar 10, 18 · #"using the "color(blue)"trigonometric identities"# #•color(white)(x)tantheta=sintheta/costheta# #•color(white)(x)sin^2thetacos^2theta=1# #rArrsintheta=sqrt(1Apr 05, 21 · 1 Find cos X and tan X if sin X = 2/3 2 In a given triangle LMN, with a right angle at M, LN MN = 30 cm and LM = 8 cm Calculate the values of sin L, cos L, and tan L


Important Trigonometric Identiti



Example 28 If Tan X 3 4 Find Sin X 2 Cos X 2 Tan X 2
Free trigonometric equation calculator solve trigonometric equations stepbystepOct 17, 18 · Trigonometric, Identities & Formulas Relation between angle and sides of the triangle, values of trigonometric functions at standardJun 23, 16 · How do you express #sin^2 theta sec^2 theta tan^2 theta # in terms of #cos theta #?



Expressing Sin X And Cos X In Terms Of T Tan X 2 Youtube



Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download
Jan 30, 07 · Write down the two formula for tan x and cos x for a right angle triangle Are there any similar terms in those equations?Apr 15, 21 · Trigonometric Functions are formed when trigonometric ratios are studied in terms of radian measure for any angle (0, 30, 90, 180, 270)These are also defined in terms of sine and cosine functions In this article, we will provide you with all the details on trigonometric functions such as value in degree, radians, complete trigonometric table and other relevant informationTo see the answer, pass your mouse over the colored area To cover the answer again, click "Refresh" ("Reload")



If Theta 30 Verify That Cos2theta 1 Tan 2theta 1 Tan 2theta Brainly In



14 2 Trigonometric Identities
Nov 24, 14 · If $\tan\theta = \frac{2t}{1t^2}$ then I would multiply by $\cos \theta$ to get $$\sin \theta = 2t\frac{\cos \theta}{1t^2}$$ but that doesn't look right trigonometry ShareThe triple angle identity of cos 3 θ \cos 3 \theta cos 3 θ can be proved in a very similar manner From these formulas, we also have the following identities for sin 3 (θ) \sin^3(\theta) sin 3 (θ) and cos 3 (θ) \cos^3 (\theta) cos 3 (θ) in terms of lower powersIn this video I want to give you the basics of trigonometry trigonometry and it sounds like a very complicated topic but you're gonna see that it's really just the study of the ratios of sides of triangles the trig part of trigonometry literally means triangle and the metry part literally means measure so let's to me let me just give you some examples here and I think it'll make everything



Solved 3 Simplitfy And Express As A Single Term Sin 8 1 Chegg Com



Trigonometric Identities Simplify Expressions Video Lessons Examples And Solutions
Double Angle Values and Trigonometric Identities The value of a cosine function is obtained when we'll divide the number {eq}1 {/eq} by the integer value of the secant function and then simplifyCos θ as `"adj"/"hyp"`, and tan θ as `"opp"/"adj"`, but we are using the specific x, y and rvalues defined by the point (x, y) that the terminal side passes through$2\sin^2\theta3\cos^2\theta=2cos^2\theta$ Because of the convenience of using the identity, $\sin^2 \theta\cos^2 \theta=1$, we didn't have to use compound angle relationship to transform the target expression into an expression involving a single trigonometric function



Solved Prove The Identitycos Theta Cos 7 Theta Sin 7 Th Chegg Com
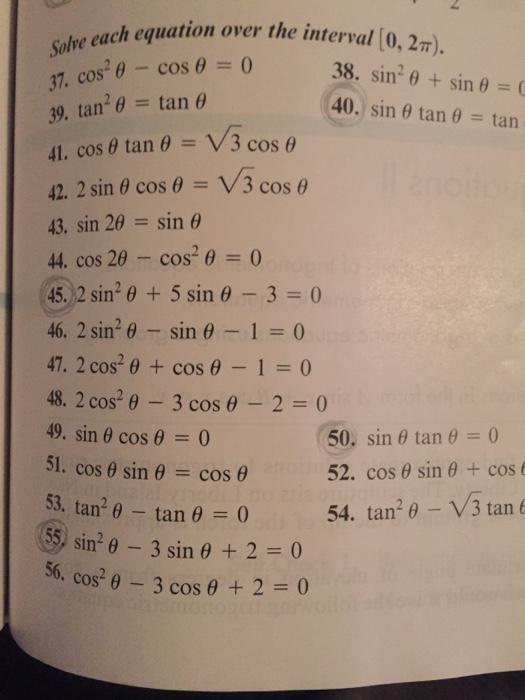


Solved Solve Each Equation Over The Interval 0 2 Pi C Chegg Com
The second shows how we can express cos θ in terms of sin θ Note sin 2 θ "sine squared theta" means (sin θ) 2 Problem 3 A 345 triangle is rightangled a) Why?Jan 31, 18 · For an angle in standard position, we define the trigonometric ratios in terms of x, y and r `sin theta =y/r` `cos theta =x/r` `tan theta =y/x` Notice that we are still defining sin θ as `"opp"/"hyp"`;Trigonometry Cosine, Sine and Tangent of Multiple Angles (Chebyshev's Method) Whilst De Moivre's Theorem for Multiple Angles enables us to compute a sine or cosine of a multiple angle directly, for the cosine we need to convert powers of sine to cosines (and similarly for the sine) However, Chebyshev's Method gives the formula in the required form for the cosine, and, for



Tan1 2 Sin 1 2x 1 X 2 Cos 1 1 Y 2 1 Y 2 X Y 1 Xy If X Lt 1 Y Gt 0 And Xy Gt 1 Mathematics Topperlearning Com Exkwfcdd



Solved Establish The Identity 1 Tan 2 Theta 1 Tan 2 Chegg Com
If you have gone through doubleangle formula or tripleangle formula, you must have learned how to express trigonometric functions ofIn various applications of trigonometry, it is useful to rewrite the trigonometric functions (such as sine and cosine) in terms of rational functions of a new variable These identities are known collectively as the tangent halfangle formulae because of the definition of These identities can be useful in calculus for converting rational functions in sine and cosine to functions of t in orderMar 01, 18 · `sin (alpha/2)=sqrt(1cos alpha)/2` Half Angle Formula Cosine Using a similar process, with the same substitution of `theta=alpha/2` (so 2θ = α) we subsitute into the identity cos 2θ = 2cos 2 θ − 1 (see cosine of a double angle) We obtain `cos alpha=2\ cos^2(alpha/2)1` Reverse the equation `2\ cos^2(alpha/2)1=cos alpha` Add 1 to
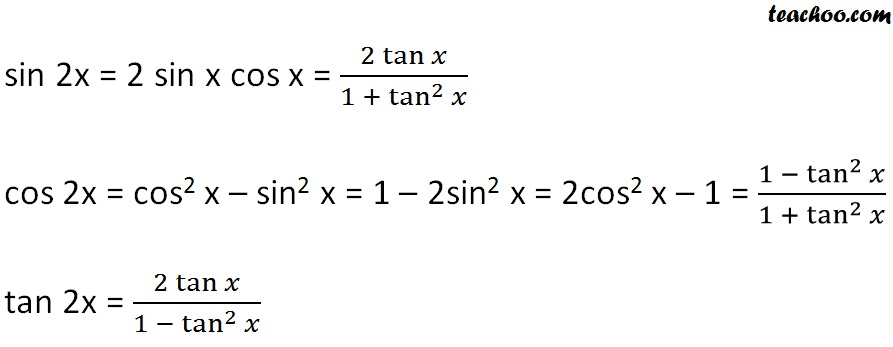


Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi


Important Trigonometric Identiti
And tanθ in terms of t, we deduce cosθ = (2t 1 t2) (2t 1 − t2) = 1 − t2 1 t2 We can also prove that cosθ = 1 − t2 1 t2 using Approaches 1 and 2 above By expressing 3 cosθ sinθ in terms of t, or otherwise, show that this expression cannot have any value between − 2√2 and 2√2 Method 1In the same way, the cosine of double angle is written in mathematical form as $\cos{2\theta}$ in trigonometry The cosine of double angle can be written in terms of sine and cosine of angle in subtraction form as follows $\cos{(2\theta)}$ $\,=\,$ $\cos^2{\theta}\sin^2{\theta}$Feb 03, 18 · \{\sin ^2}\left( \theta \right) {\cos ^2}\left( \theta \right) = 1\ Note that this is true for ANY argument as long as it is the same in both the sine and the cosine



Revision Trigonometry Siyavula


What Is The Formula Of Tan2x Quora
Mar 23, 21 · or, tan theta = sin theta/cos theta (here, theta is an angle) The sine of an angle is equal to the length of the opposite side divided by the length of the hypotenuse side, while the cosine of an angle is the ratio of the adjacent side to the hypotenuse side Hence, sin x = Opposite Side/Hypotenuse Side cos x = Adjacent Side/Hypotenuse SideIntroduction to Tan double angle formula let's look at trigonometric formulae also called as the double angle formulae having double angles Derive Double Angle Formulae for Tan 2 Theta \(Tan 2x =\frac{2tan x}{1tan^{2}x} \) let's recall the addition formulaThe range of cscx is the same as that of secx, for the same reasons (except that now we are dealing with the multiplicative inverse of sine of x, not cosine of x)Therefore the range of cscx is cscx ‚ 1 or cscx • ¡1 The period of cscx is the same as that of sinx, which is 2Since sinx is an odd function, cscx is also an odd function Finally, at all of the points where cscx is
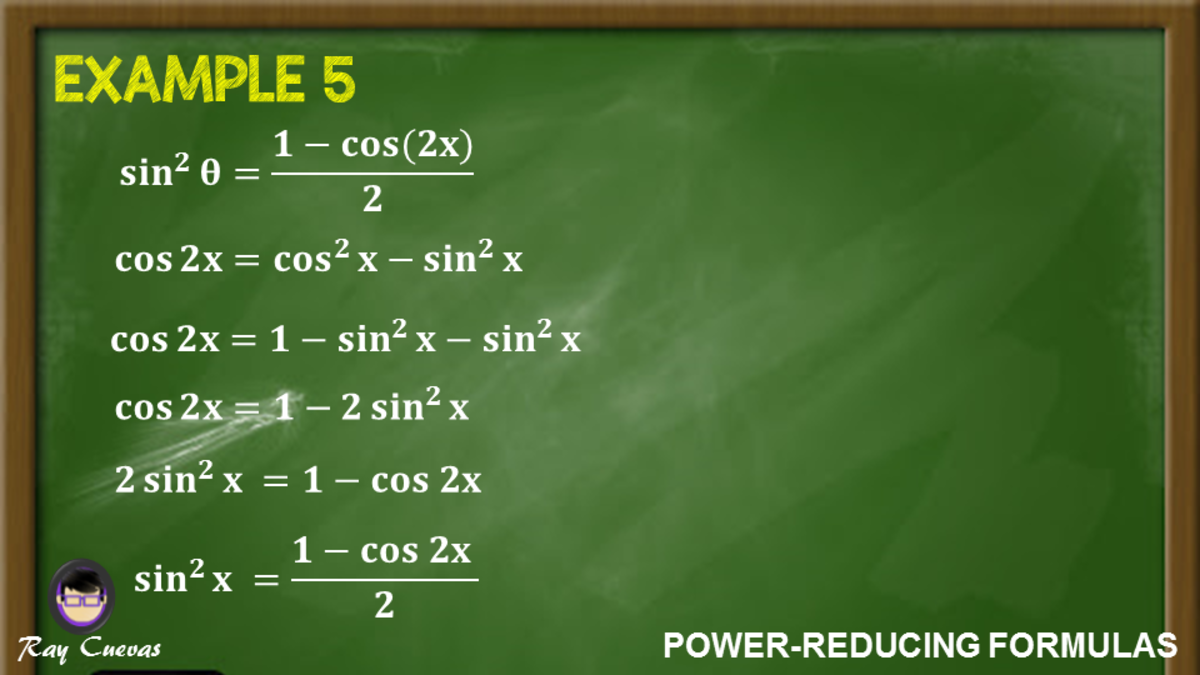


Power Reducing Formulas And How To Use Them With Examples Owlcation


How Do You Verify Tan 28 Sin 28 Tan 28sin 28 Socratic
We can talk about the range as for any value inputted as theta cos of theta would give us values from 1 to 1 now, cos(theta)=cos(theta) so cos(1)=cos(1)=minimum of the function =Trigonometric function of cos 2A in terms of tan A is also known as one of the double angle formula We know if A is a number or angle then we have, cos 2A = cos2 A sin2 A cos 2A = c o s 2 A − s i n 2 A c o s 2 A ∙ cos2 ASin Cos Tan Chart Though we can find the values of cos, sin, and tan using the calculator, there is a chart with some standard angles 0 o, 30 o, 45 o, 60 o, and 90 o Tips to remember sin cos tan



How Do You Use Double Angle Identities To Solve Equations Socratic


How To Use The Excel Tan Function Exceljet
Finding the Derivative of Inverse Cosine Function, $\displaystyle{\frac{d}{dx} (\arccos x)}$ The process for finding the derivative of $\arccos x$ is almost identical to that used for $\arcsin x$Tan(x) is an odd function which is symmetric about its origin tan(2x) is a doubleangle trigonometric identity which takes the form of the ratio of sin(2x) to cos(2x) sin(2 x ) = 2 sin( x ) cosDec , 16 · To get the formula for tan 2A, you can either start with equation 50and put B = A to get tan(A A), or use equation 59for sin 2A / cos 2nd


Is Tan 2x Equal To Tan X 2
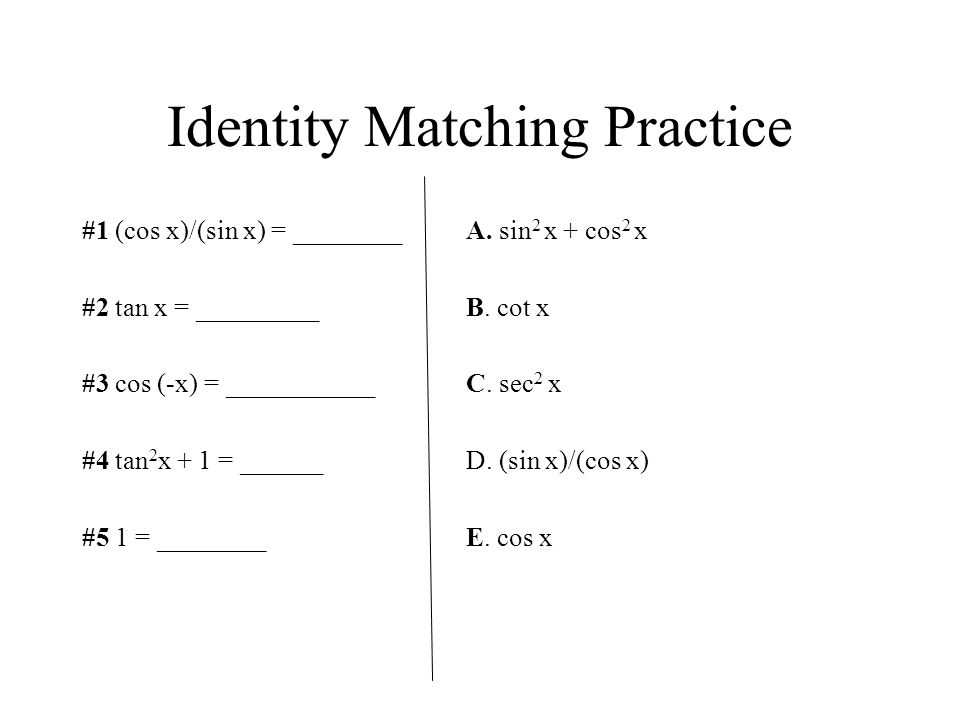


5 1 Fundamental Trig Identities Sin 1cos 1tan 1 Csc Sec Cot Csc 1sec 1cot 1 Sin Cos Ppt Download
And then, the first of these formulae becomes Cos(t t) = Cos t cos t – Sin t sin t so that Cos 2t = Cos 2 t – Sin 2 t And this is how we get second doubleangle formula, which is so called because you are doubling the angle (as in 2A) Practice Example for Cos 2 Solve the equation cos 2a = sin a, for – Π \(\leq\) a< ΠThe trigonometric function are periodic functions, and their primitive period is 2 π for the sine and the cosine, and π for the tangent, which is increasing in each open interval (π /2 k π, π /2 (k 1) π) At each end point of these intervals, the tangent function has a vertical asymptoteIn a way, sine and tangent double angles are very easy because there's only one formula for them Cosine 2 θ \theta θ is actually the tricky one because when you see a question, you don't know whether to use the first, the second or the third expression But don't worry too much because since you have three versions of cosine to choose from, you'll actually be able to make your



Art Of Problem Solving



Powers Of Trigonometric Functions
Use Reduction Formulas to Simplify an Expression The doubleangle formulas can be used to derive the reduction formulas, which are formulas we can use to reduce the power of a given expression involving even powers of sine or cosineThey allow us to rewrite the even powers of sine or cosine in terms of the first power of cosineIdentify restricted values of \(\theta\) We know that \(\tan \theta\) is undefined for \(\theta = \text{90} ° k \cdot \text{180} °, k \in \mathbb{Z}\) Note



How To Write Double Angle Formula Sin 2x In Terms Of Tan X Youtube
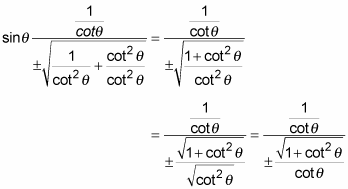


Express Sine In Terms Of Cotangent Dummies



Power Reducing Formulas And How To Use Them With Examples Owlcation
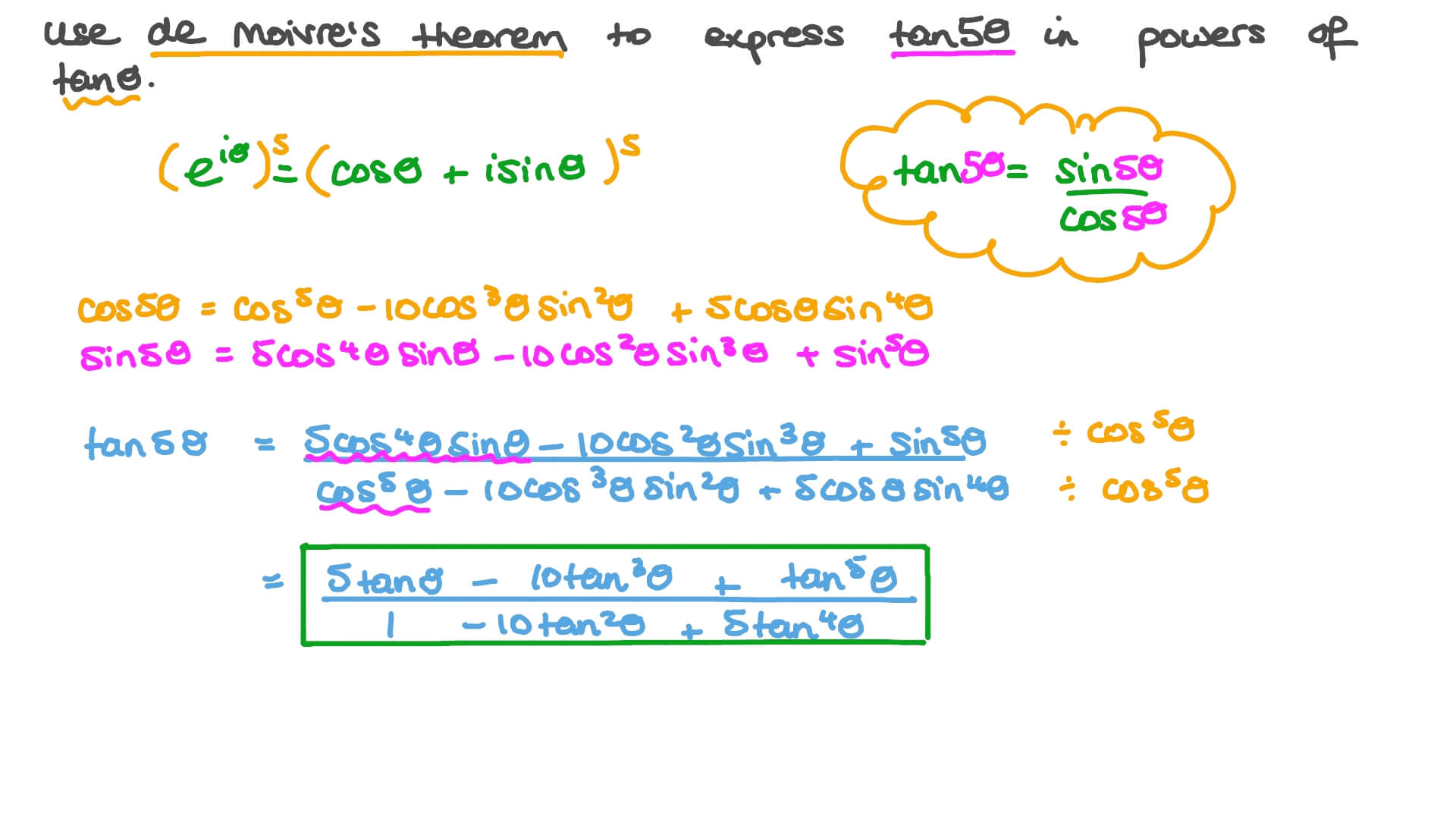


Question Video Using De Moivre S Theorem To Derive Trigonometric Identities Nagwa



Tangent Half Angle Formula Wikipedia



B Mathematics 7 Show That The Axes Are To Be Rotated In Rotated Through An
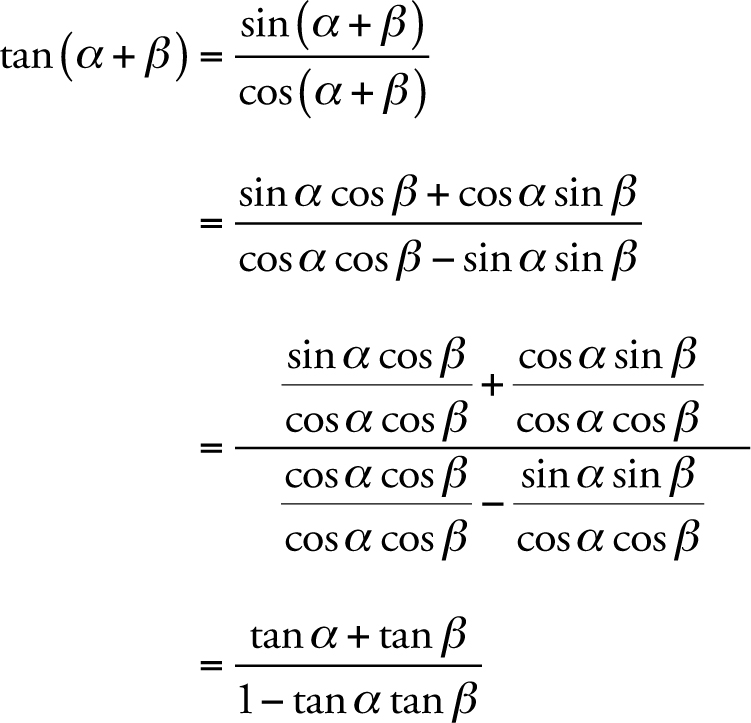


Tangent Identities


What Is The Formula Of Tan2x Quora
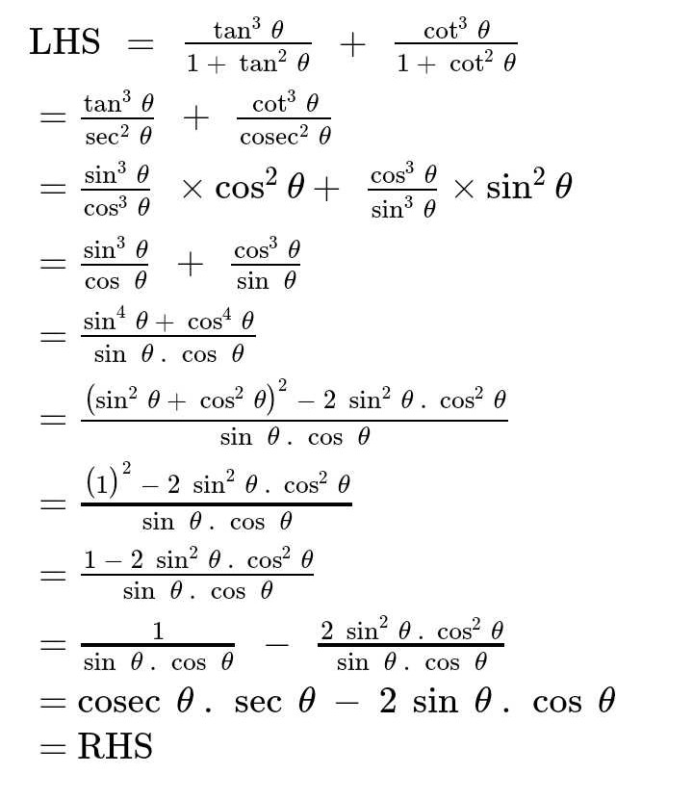


Prove If Tan 3 Theta 1 Tan 2 Theta Cot 3 Theta 1 Cot 2 Theta Sec Theta Cosec Theta 2 Sin Theta Cos Theta Edurev Class 10 Question
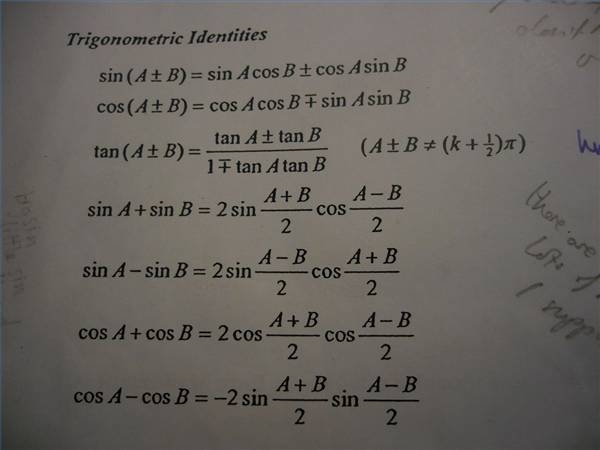


What Are Reciprocal Identities


How I Remember Trig Identities Part 2 Beyond Solutions



General Solution Of Tan 5 Theta Cot 2 Theta Is Youtube


Summary Of Trigonometric Identities



Prove That Tan Squared Theta Minus Sin Square Theta Sin Square Theta Tan Square Theta Maths Introduction To Trigonometry Meritnation Com
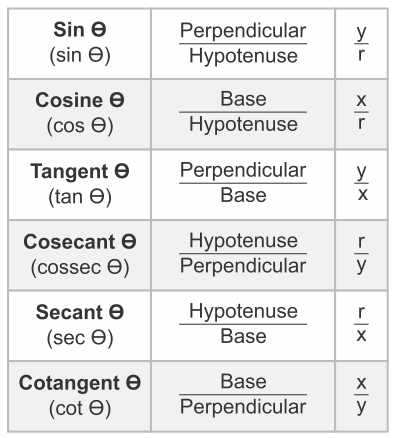


Trigonometric Ratios Table Formulas Definitions Mnemonics Problems



Ex 3 3 19 Prove Sin X Sin 3x Cos X Cos 3x Tan 2x



Lesson 24 Double Angle Half Angle Identities Ppt Video Online Download



How To Write Double Angle Formula Sin 2x In Terms Of Tan X Youtube


Summary Of Trigonometric Identities



Trigonometric Identities Topics In Trigonometry



Using Trig Angle Addition Identities Manipulating Expressions Video Khan Academy
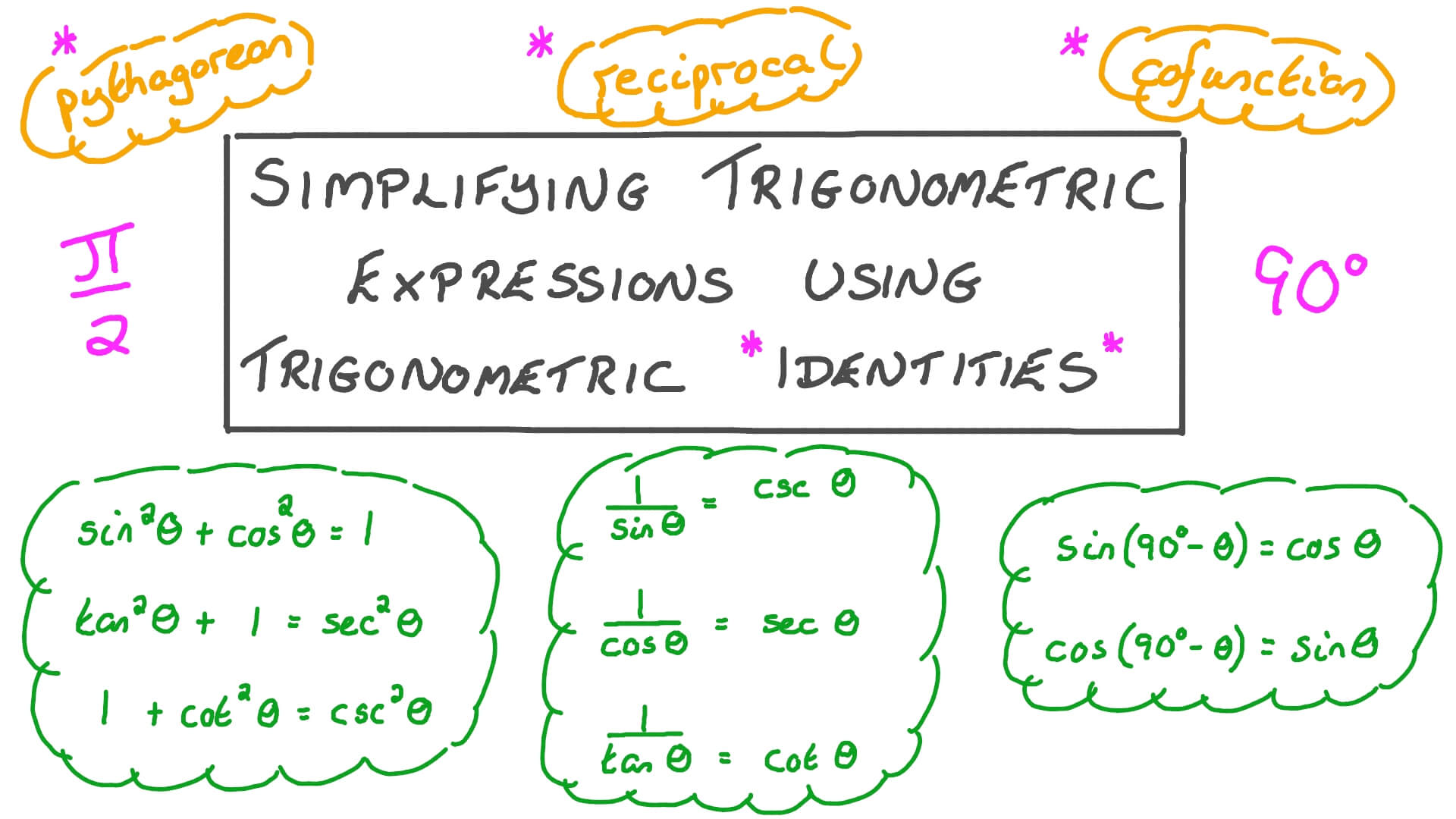


Lesson Video Simplifying Trigonometric Expressions Using Trigonometric Identities Nagwa


What Is The Formula Of Tan2x Quora


Important Trigonometric Identiti



How To Prove Quotient And Reciprocal Identities Studypug



Write Cos2x In Tan And Prove Trigonometric Identity For Double Angle Youtube
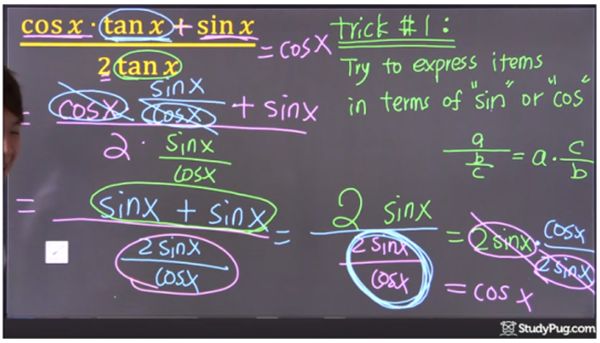


How To Prove Quotient And Reciprocal Identities Studypug



Complete The Following Activity By Filling The Boxes Sin 2



Tangent Half Angle Formula Wikipedia



If Tan 2 Theta 1 2 Tan 2 Phi Prove That Cos 2 Phi 1 2 Cos 2
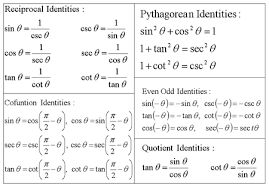


Trigonometric Identities Mathematics Quiz Quizizz



Cofunction Identities In Trigonometry With Proof And Examples Owlcation



Tangent Identities



14 2 Trigonometric Identities


What Is The Formula Of Tan2x Quora



Lesson 24 Double Angle Half Angle Identities Ppt Video Online Download


Trigonometric Functions Expressed By The Tangent Of The Half Angle Trigonometric Identities



Tangent Half Angle Formula Wikipedia


What Are The Formulas Of Cos 2x Quora



How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic



Write Cos2x In Terms Of Tanx Double Angle Transformation Youtube



Misc 8 Tan X 4 3 Find Sin X 2 Cos X 2 And Tan X 2



Prove That Tan2 Theta Tan 2 Theta 1 Cosec 2 Theta Sec 2 Theta Cosec 2 Theta 1 Sin 2 Theta Cos2 Brainly In


Tan2x ただの悪魔の画像



If 1 Sin 2 Theta 3 Sin Theta Cos Theta Then Prove That Tan Theta 1 Or 1 2 Brainly In


Cochranmath Solving Trigonometric Equations



Tangent Half Angle Formula Wikipedia
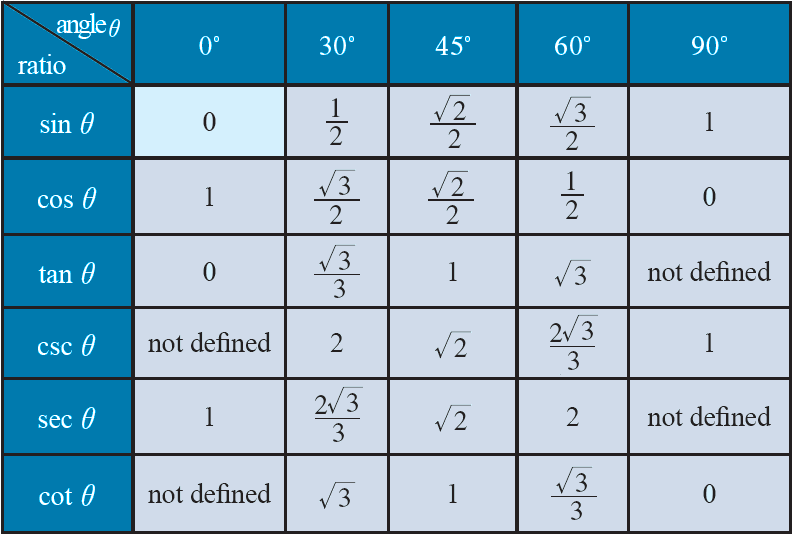


Trigonometric Formulas



Ex 8 4 2 Write All Trigonometric Ratios In Terms Of Sec A



Prove That Tan 2 Theta Sin 2 Theta Tan 2 Theta Sin 2 Theta



If 1 Sin 3 Sin Cos Then Show That Tan 1 Or 1 2 Mathematics Topperlearning Com 328h6ymm


Derivatives Of Trigonometric Functions



Introduction To Trigonometry Ncert Solutions For Class 10 Maths Edusaint


Analytic Trigonometry


Trigonometric Integrals



Summary Of Trigonometric Identities



How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic
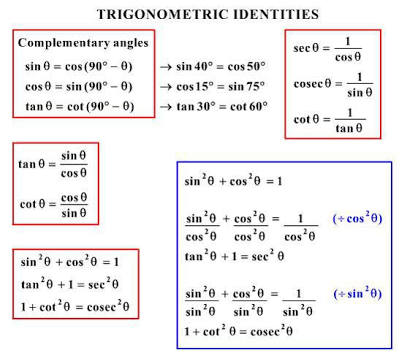


How Do You Simplify The Expression Sin 2theta Cos 2theta Cos 2theta Socratic



Trigonometry Definition Formulas Ratios Identities Britannica


Cbse 10 Math Cbse Introduction To Trigonometry Ncert Solutions



Solved Letting Y Tan 4 Theta And X Tan Theta Express Chegg Com


Summary Of Trigonometric Identities


1 Sin2 Theta 3 X Sin Theta X Cos Theta Introduction To Trigonometry Maths Class 10



Prove That Tan 2 2theta Tan 2 Theta 1 Tan 2 2theta Tan 2 Th



21 Differentiation And Integration Of Trigonometry Function 9709


The Trigonometric Ratios Of Angl



Solved Prove The Following Identities Tan 2theta 2 Tan Chegg Com



14 2 Trigonometric Identities



Trigonometric Functions Introduction Sine Cosine Videos And Examples



Introduction To Trigonometry Ncert Solutions For Class 10 Maths Edusaint


Prove The Identity Cos 2x 1 Sin 2x Tan P 4 X Sarthaks Econnect Largest Online Education Community



Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf



0 件のコメント:
コメントを投稿